■セントとは?
セントとは、音程を表す単位です。つまり、2つの音の高さがどれくらい離れているかを示す数字ですね。
一般的な音律である平均律の上では、半音の間隔を100セントとして定義されます。
例えば、
最近接のドとド#の音程(音の高さの差)は100セント、レとミの音程は200セント、ミとソの音程は300セント、1オクターブ差の2音の音程は1200セント、といった具合です。
セント値は、音律の定義などのやや学問的なフィールドや調律に関する内容で使用されることが多く、普段楽器をプレーする上では使用することはほとんどありません。
■セントを使うメリット
音程を数字で表す方法
以下の記事でも言及していますが、音の高さはその音の周波数によって決まり、周波数が大きいほど音が高くなります。
【記事】音の高さと周波数 〜基準は440Hz?442Hz?〜
つまり、音程の数字で表すには、周波数を用いる方法もあります。では、周波数での数値表現に対して、セント値を用いるのにはどんなメリットがあるでしょうか?
(音程の度数表記はセント値とは目的や用法が全く異なるためここでは割愛します。)
周波数とセント値の比較
平均律の上では、音の高さが半音上がると周波数は約1.059倍(2の12乗根倍)になります。これを12回繰り返すと元の周波数の2倍、つまり1オクターブ上の音になります。
ここでポイントは、所定の量(半音◯個分)だけ音の高さが変わるとき、周波数は掛け算で決まるという点です。足し算ではないんですね。
わかりやすくするために、周波数とセント値の数直線の上に、半音刻みで音をとってみると以下のようになります。
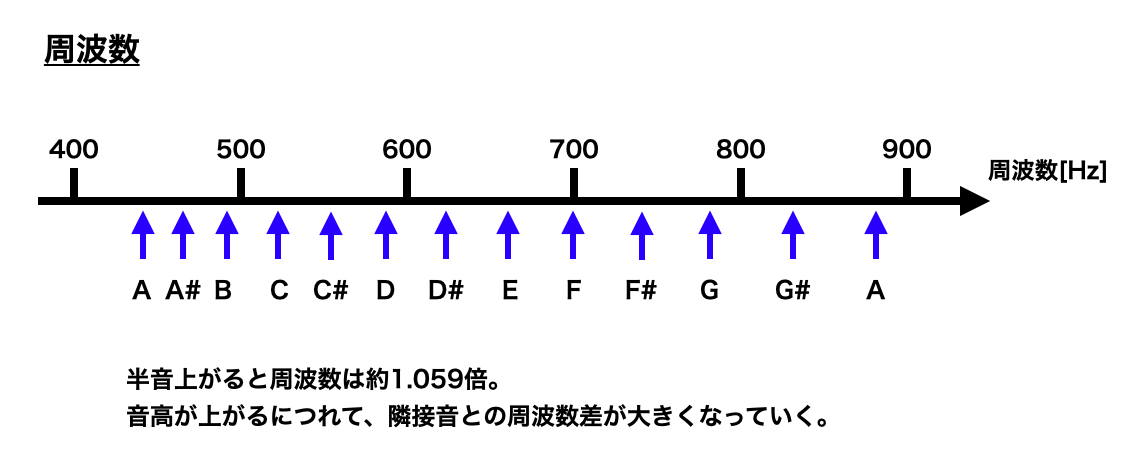
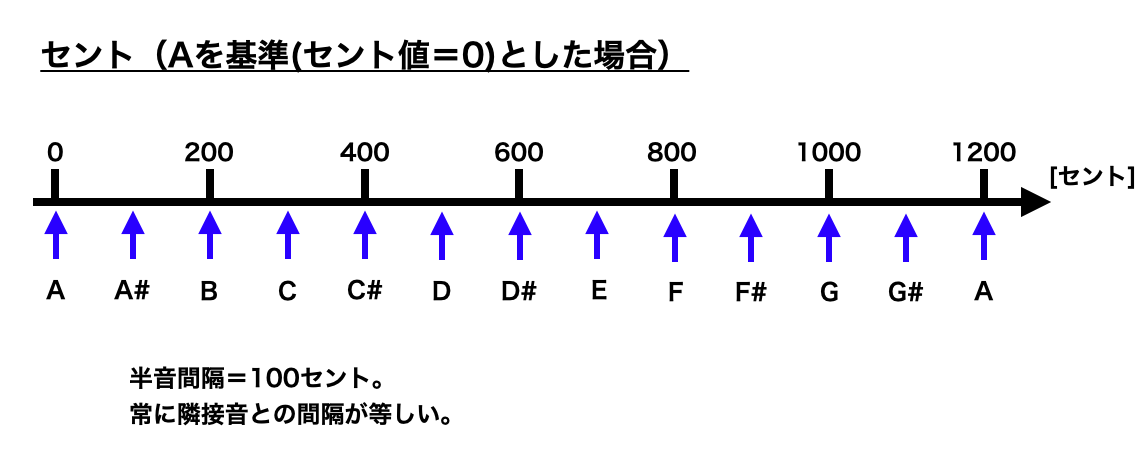
周波数の軸の上では各音が等間隔になりません。そのため、音程を表現するとき、周波数を用いると直感的に理解しにくいというデメリットがあります。
一方、これを補うのがセント値です。セント値の軸の上では、各音が等間隔に並びます。例えば「半音間隔であれば、どこの半音でも同じ数字にしたほうがいいよね」といって定義されたのがこの「セント」という単位であるというわけですね。
■セントの定義
セント値は以下のような式で定義されますが、要は半音の間隔を100セントとするということです。
定義式
2つの音の周波数をa,bとすると(a>b)、その2音の間隔を示すセント値nは以下の式で定義される。
n = 1200・log2(b/a)
繰り返しになりますが、音律や調律に関する記述では、半音より小さい音程に言及する必要があり、セント値がたびたび使われることがあります。

